About me and why I created this physics website.

Engineering Mechanics Problems

On this page I give lots of examples of solved engineering mechanics problems, typical for college/university courses in engineering. They are provided as handwritten PDF files which you can conveniently download. This will be very useful when studying for tests and exams. The aim here is to cover many different types of problems, from easy to difficult, to help you study and prepare more effectively. I know that getting access to lots of good problems and their solutions can sometimes be difficult, which is why I created this page, so you have a lot of problems and their solutions all in one convenient place. All these example problems are my own creation, so you won't find an exact copy of them anywhere else. In order to keep them relevant to your courses, I have referenced commonly used engineering mechanics books to get ideas and inspiration for problems (such as books written by Hibbeler and Beer/Johnston). So there will of course be similarities between them and the problems you will encounter in your classes and physics books.

The example problems are all uniquely numbered for easy reference. The problem statement is given, and then the solution is provided as a PDF file which you can download.

If you want to review the theory behind all these problems, I conveniently cover that on this website, in the kinematics and dynamics pages. Note that this page is a work in progress and new content will be added regularly (however, the kinematics sections are completed).

To see the example problems click on the category you are interested in:

Kinematics – Curvilinear motion problems involving normal and tangential components
Kinematics – Curvilinear motion problems involving radial and transverse components
Kinematics – Problems involving instant center
Kinematics – 2-D problems involving relative-motion analysis with rotating axes
Kinematics – 2-D problems involving relative-motion analysis with acceleration
Kinematics – 3-D problems involving general motion


Kinematics – Curvilinear motion problems involving normal and tangential components

Problem # 1:



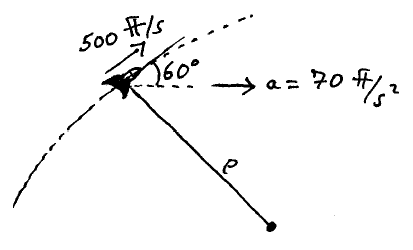
A jet aircraft is flying along an arc, and at the instant shown it has a speed of 500 ft/s and an acceleration of 70 ft/s² in the direction shown. What is the rate of increase in the speed of the plane, and the radius of curvature ρ of the arc, at the instant shown?

Download solution

Problem # 2:



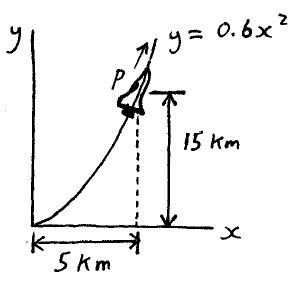
A jet aircraft flies along a vertical parabolic path, and at point P it has a speed of 260 m/s, which is increasing at a rate of 0.9 m/s². Determine the magnitude of the acceleration at point P.

Download solution

Problem # 3:



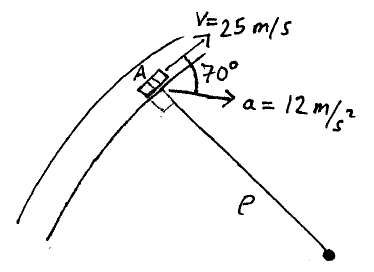
At a certain instant, a car at A has a speed of 25 m/s and an acceleration of 12 m/s² acting in the direction shown. Calculate the radius of curvature ρ of the car's path and the rate of increase in the speed of the car.

Download solution

Problem # 4:



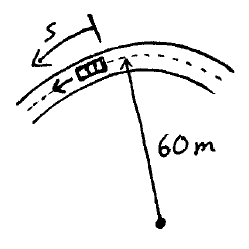
A car travels at a speed of 8 m/s along a circular road which has a radius of 60 m. Starting from s = 0, where s is the travel distance, in meters, the car increases its speed by dv/dt = (0.07s) m/s². Calculate the speed of the car and the magnitude of its acceleration when s = 12 m.

Download solution

Problem # 5:



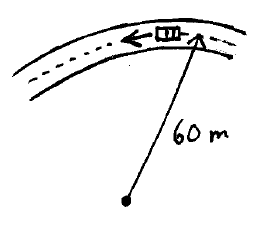
A car travels at a speed of 8 m/s along a circular road which has a radius of 60 m. Starting from a time of t = 0, in seconds, the car increases its speed by dv/dt = (0.6t) m/s². Calculate the speed of the car and the magnitude of its acceleration when t = 5 s.

Download solution

Problem # 6:

The position of a particle is defined by r = (t² + t)i + (2e^tsin 2t)j ft, where t is in seconds and the argument for sine is in radians. When t = 3 s, determine the speed of the particle and its normal and tangential components of acceleration.

Download solution

Problem # 7:

A particle travels along a path such that its acceleration is defined by a = 18i + 2tj ft/s². The particle starts from rest at r = 0. When t = 8 s, calculate the speed of the particle and the radius of curvature of its path.

Download solution

Problem # 8:



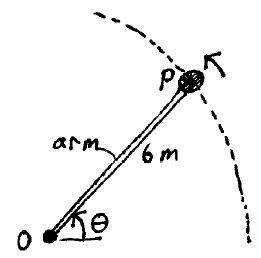
An arm rotates about a pivot O, and its end P speed increases according to the equation dv/dt = 0.6e^t + 2t, where t is in seconds. The arm starts from rest at θ = 0, and the length of the arm is 6 m. Determine the normal and tangential components of the velocity and acceleration of the end P when θ = 35°.

Download solution

Problem # 9:



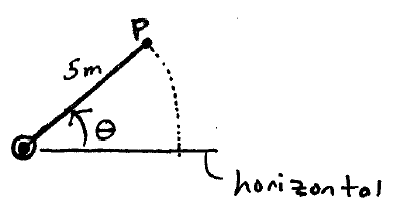
A particle P is traveling along a circular arc of radius 5 m. The speed of the particle is given by v = 0.5e^tsin 2t m/s, where t is in seconds and the argument for the sine is in radians. Determine the magnitude and direction of the acceleration of P when t = 2.5 s. The particle starts from rest when θ = 0°.

Download solution

Kinematics – Curvilinear motion problems involving radial and transverse components

Problem # A-1:



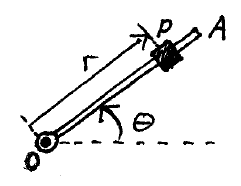
The rod OA is rotating in a horizontal plane about point O such that θ = 2t³, where t is in seconds. At the same time, the collar P is sliding outward along the rod such that r = 40t². Determine the magnitude of the velocity and acceleration of the collar when t = 1.5 s. Distances are measured in mm, and angles in radians.

Download solution

Problem # A-2:



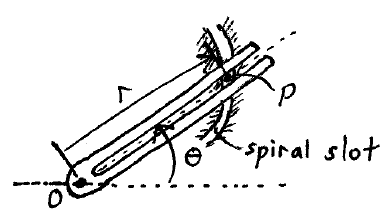
A slotted link rotates about point O with a constant angular velocity dθ/dt = 4 rad/s. As a result of this motion, a peg P is being pushed along a spiral slot defined by r = 0.3θ meters, where θ is in radians. Determine the radial and transverse components of the velocity and acceleration of P at the instant when θ = π/3 radians.

Download solution

Problem # A-3:



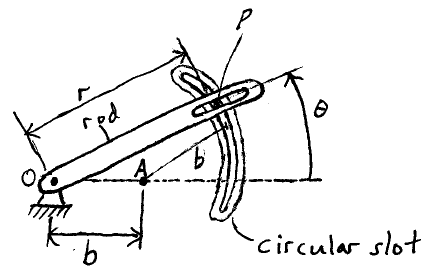
A rod is rotating about a point O, while pushing a pin P along a circular slot, as shown. The pin P is also free to slide along a slot in the rod, as shown. If the rod rotates at constant rate dθ/dt, show that the acceleration of P has constant magnitude, and determine the direction of this acceleration.

Download solution

Problem # A-4:



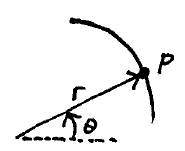
For a short distance, a particle P travels along a path defined by r = 200/θ m, where θ is in radians. If dθ/dt is constant and equal to 0.3 rad/s, calculate the radial and transverse components of the velocity and acceleration of the particle when θ = 5π/4 radians.

Download solution

Problem # A-5:



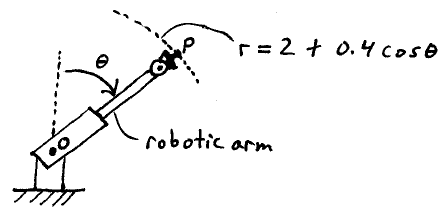
A robotic arm with end point P rotates about point O, while also changing its length such that the distance from point O to point P is given by r = 2 + 0.4cos θ meters. What is the greatest constant angular velocity of the arm, dθ/dt, so that the maximum acceleration of P is 6 m/s². Calculate the answer over the range −45° ≤ θ ≤ 45°.

Download solution

Problem # A-6:



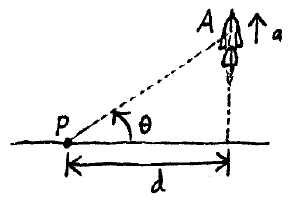
A rocket is launched vertically upward and at a given instant makes an angle of θ with the ground, as measured from point P. If the acceleration of the rocket is a at the instant shown, determine the acceleration of the rocket in terms of d, θ, dθ/dt, and d²θ/dt².

Download solution

Problem # A-7:



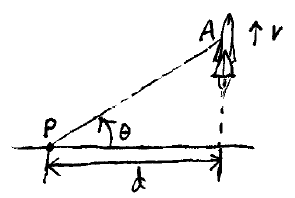
A rocket is launched vertically upward and at a given instant makes an angle of θ with the ground, as measured from point P. If the speed of the rocket is v at the instant shown, determine the speed of the rocket in terms of d, θ, and dθ/dt.

Download solution

Kinematics – Problems involving instant center

Problem # B-1:



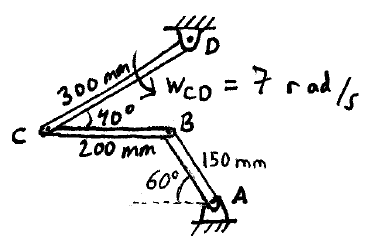
If link CD is rotating at w_CD = 7 rad/s in the arrangement shown, what is the angular velocity of links AB and BC at the instant shown?

Download solution

Problem # B-2:



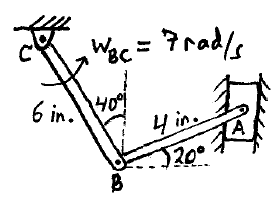
For the arrangement shown, determine the speed of block A.

Download solution

Problem # B-3:



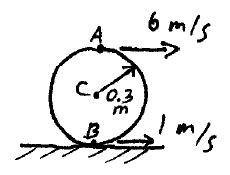
A wheel rolls with slipping on a surface, and as a result, the top and bottom of the wheel have a velocity of 6 m/s and 1 m/s, respectively. Determine the velocity of the center C of the wheel.

Download solution

Problem # B-4:



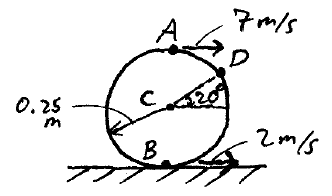
A wheel rolls with slipping on a surface, and as a result, the top and bottom of the wheel have a velocity of 7 m/s and 2 m/s, respectively. Determine the velocity of the center C and point D on the wheel.

Download solution

Problem # B-5:



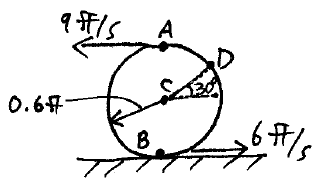
A wheel rolls with slipping on a surface, and as a result, the top and bottom of the wheel have a velocity of 9 ft/s and 6 ft/s, respectively. Determine the velocity of the center C and point D on the wheel.

Download solution

Problem # B-6:



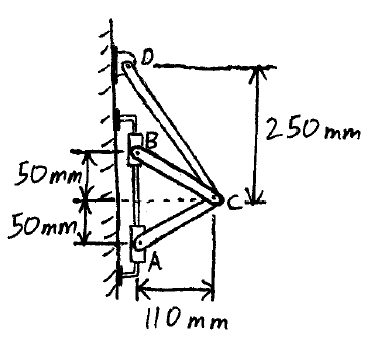
In the assembly shown, A and B are collars which are free to slide along the vertical rod shown. The velocity of collar B is 520 mm/s in the downward direction. Calculate (a) the velocity of collar A, and (b) the angular velocity of link CD.

Download solution

Problem # B-7:



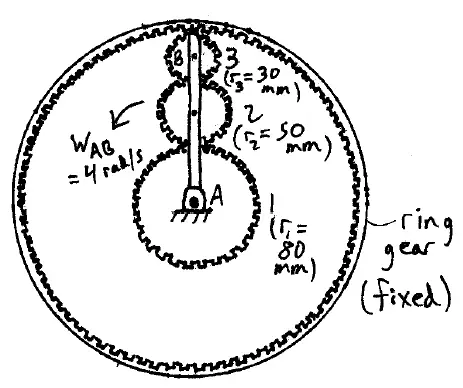
In the gear arrangement shown, the link AB has an angular velocity of w_AB = 4 rad/s. Determine the angular velocities of gears 1, 2, and 3.

Download solution

Kinematics – 2-D problems involving relative-motion analysis with rotating axes

Problem # C-1:



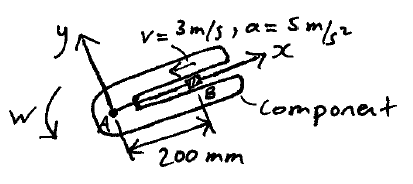
A block B is moving along a slot at a velocity of 3 m/s relative to the slot and at an acceleration of 5 m/s² relative to the slot, in the direction shown. The component containing the slot is rotating about point A at a constant angular velocity of w = 6 rad/s. Determine the acceleration of the block B at the instant shown.

Download solution

Problem # C-2:



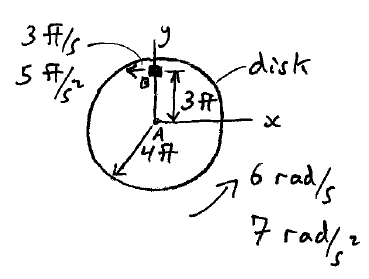
A block B is moving along a rotating disk in the direction shown with a velocity of 3 ft/s and an acceleration of 5 ft/s² relative to the disk. The disk is also rotating in the direction shown with an angular velocity of 6 rad/s and an angular acceleration of 7 rad/s². Determine the velocity and acceleration of the block.

Download solution

Problem # C-3:



A rod in the shape of a circular arc rotates about A such that a pin pushing against the rod, as shown, is moving to the right at a constant speed of 85 mm/s. Determine the angular velocity and angular acceleration of the rod at the instant shown. Note that the pin is sliding along the rod.

Download solution

Problem # C-4:



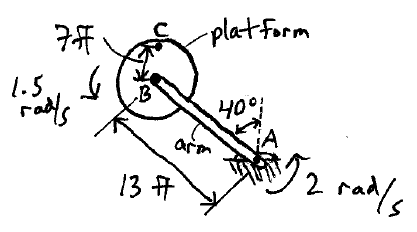
In an amusement park ride, the main arm is rotating about A at a constant angular velocity of w_a = 2 rad/s. A platform is attached to the main arm and rotates about point B due to a motor which rotates at a constant rotational speed of 1.5 rad/s. A person is sitting on the platform at point C. At the instant shown, what is the velocity and acceleration of the person?

Download solution

Problem # C-5:



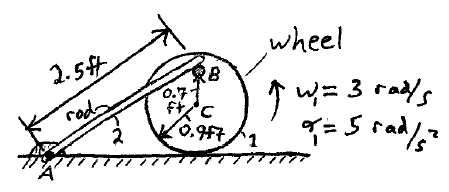
A wheel is rolling as shown without slipping. The pin B on the wheel is pushing against and sliding along the rod which is free to pivot about point A. What is the angular velocity and angular acceleration of the rod?

Download solution

Problem # C-6:



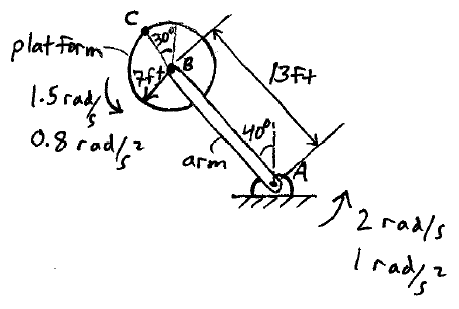
In an amusement park ride, the main arm is rotating about A with an angular velocity of w_a = 2 rad/s and angular acceleration of α_a = 1 rad/s². A platform is attached to the main arm and rotates about point B due to a motor which rotates with a rotational speed of 1.5 rad/s and a rotational acceleration of 0.8 rad/s². A person is sitting on the platform at point C. At the instant shown, what is the velocity and acceleration of the person?

Download solution

Kinematics – 2-D problems involving relative-motion analysis with acceleration

Problem # D-1:



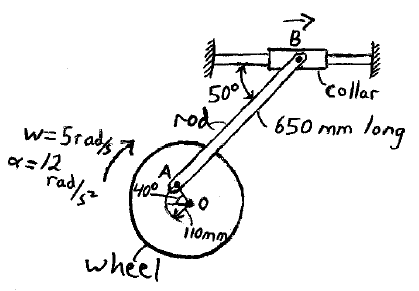
At the instant shown, a wheel and rod mechanism is in motion with dimensions and angular motions as shown. Calculate the acceleration of the collar B at this instant.

Download solution

Problem # D-2:



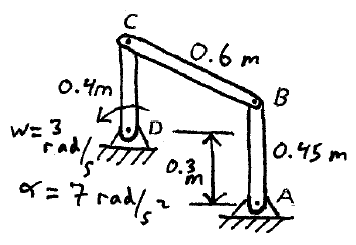
For the linkage arrangement shown, what is the angular acceleration of links AB and BC at the instant shown.

Download solution

Problem # D-3:



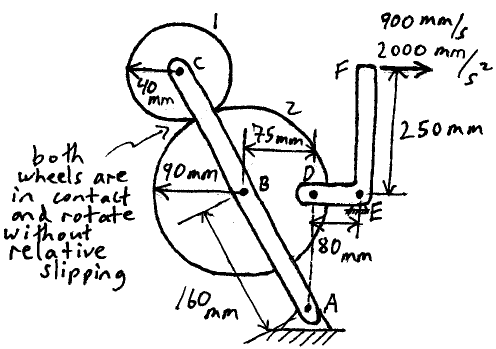
In the arrangement shown, determine the angular velocity and angular acceleration of wheel 1, wheel 2, and link AC, at the instant shown.

Download solution

Problem # D-4:



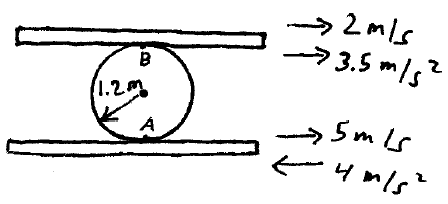
At the instant shown, a cylinder is supported between two boards, and each board is moving with the velocity and acceleration shown. Determine the angular velocity and angular acceleration of the cylinder.

Download solution

Problem # D-5:



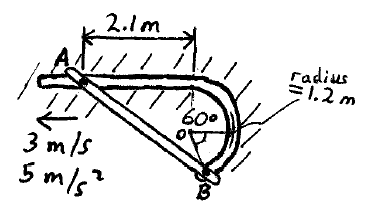
The rod AB has endpoints at A and B which are free to move in the groove shown. Calculate the angular velocity and angular acceleration of the rod at the instant shown.

Download solution

Problem # D-6:



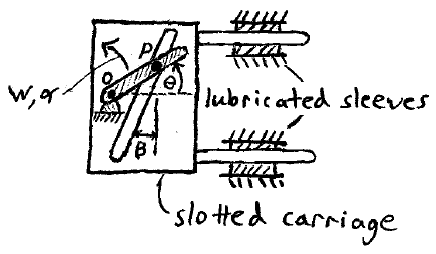
A slotted carriage is free to slide back and forth using lubricated sleeves as support, as shown. A rotating link OP is the driver of this motion. The distance between O and P is d, and the slot makes an angle of β with the vertical. Derive an expression for the velocity and acceleration of the carriage.

Download solution

Problem # D-7:



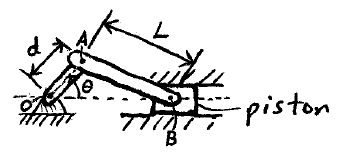
A crank OA rotates counterclockwise at an angular velocity w and an angular acceleration α. Derive an expression for the velocity and acceleration of the piston.

Download solution

Problem # D-8:



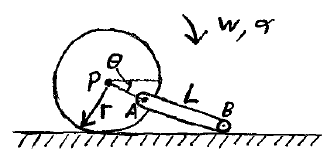
A wheel rolls without slipping on a flat surface with an angular velocity w, and an angular acceleration α. A rod is attached at point A and has a roller attached on the other end, at point B. The wheel has radius r and the rod has length L. What is the velocity and acceleration of point B when θ = 0° ?

Download solution

Kinematics – 3-D problems involving general motion

Problem # E-1:



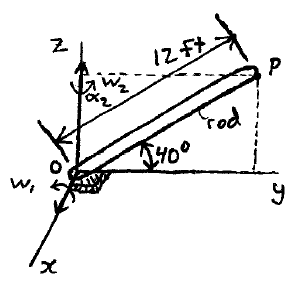
A rod is rotating about the z-axis with an angular velocity w₂ = 0.25 rad/s, and an angular acceleration α₂ = 0.52 rad/s². At the same time, the rod is rotating upward at an angular velocity w₁ = 0.7 rad/s, which is constant. At the instant shown, calculate the velocity and acceleration of point P at the end of the rod.

Download solution

Problem # E-2:



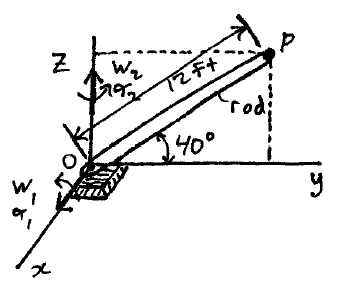
A rod is rotating about the z-axis with an angular velocity w₂ = 0.25 rad/s, and an angular acceleration α₂ = 0.43 rad/s². At the same time, the rod is rotating upward at an angular velocity w₁ = 0.7 rad/s, and an angular acceleration α₁ = 0.35 rad/s². At the instant shown, calculate the velocity and acceleration of point P at the end of the rod.

Download solution

Problem # E-3:



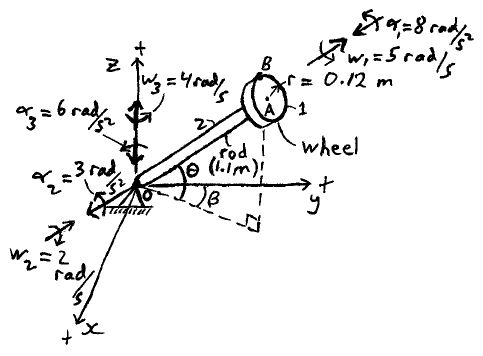
A gyrotop is rotating as shown. The wheel on the end of the rod is being rotated with a motor which rotates with an angular velocity of w₁ = 5 rad/s and an angular acceleration of α₁ = 8 rad/s², in the rotational directions shown. At the same time, the rod attached to the wheel (OA) makes an angle θ = 65° with the xy-plane, and an angle β = 35° with the y-axis, as shown. The angle θ decreases at the rate w₂ = 2 rad/s, and the angular acceleration of θ is 3 rad/s², in the rotational directions shown. Lastly, the angle β decreases at the rate w₃ = 4 rad/s, and the angular acceleration of β is 6 rad/s², in the rotational directions shown. If the radius of the wheel is 0.12 m, what is the velocity and acceleration of the topmost point of the wheel (point B)?

Download solution

Problem # E-4:



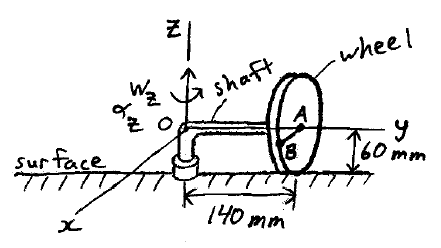
A wheel rolls along a level surface without slipping. The wheel rotates on a shaft, and the shaft rotates about point O with an angular velocity of w_z = 4 rad/s and an angular acceleration of α_z = 3 rad/s². Determine the velocity and acceleration of point B on the wheel, at the instant shown.

Download solution

Problem # E-5:



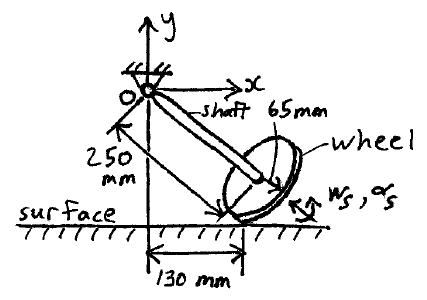
A wheel rolls along a level surface without slipping. The wheel is connected to a shaft which has a ball-and-socket joint at O, around which the shaft and wheel rotate, with a spin angular velocity of w_s = 7 rad/s and a spin angular acceleration of α_s = 3 rad/s². Determine the angular velocity and angular acceleration of the wheel, at the instant shown.

Download solution

Problem # E-6:



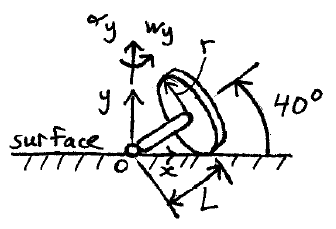
A wheel rolls along a level surface without slipping. The wheel is connected to a shaft which has a ball-and-socket joint at O, around which the shaft and wheel rotate. The wheel and shaft precess around point O, with an angular velocity of w_y = 6 rad/s, and an angular acceleration of α_y = 2 rad/s². Determine the angular velocity and angular acceleration of the wheel, at the instant shown.

Download solution

Problem # E-7:



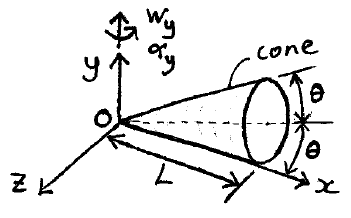
A cone rolls on the xz-plane without slipping, with its tip at the origin O, around which the cone rotates. The cone precesses around point O, with an angular velocity w_y, and an angular acceleration α_y. Determine the angular velocity and angular acceleration of the cone, at the instant shown.

Download solution

Problem # E-8:



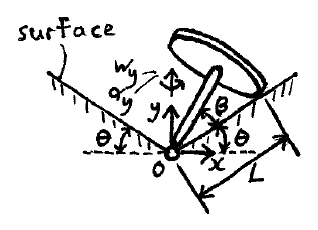
A wheel rolls along a conical surface without slipping. The wheel is connected to a shaft which has a ball-and-socket at O, around which the shaft and wheel rotate. The wheel and shaft precess around point O, with an angular velocity of w_y, and an angular acceleration of α_y. Determine the angular velocity and angular acceleration of the wheel, at the instant shown.

Download solution

Problem # E-9:



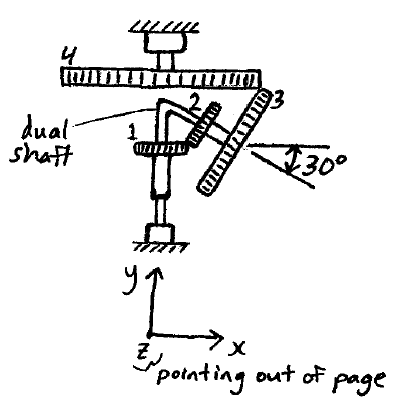
In the gear system shown, gear 4 rotates with an angular velocity w₄ and an angular acceleration α₄, with rotation vector pointing along the negative y-direction. Gear 1 rotates with an angular velocity of w₁ and an angular acceleration of α₁, with rotation vector pointing along the negative y-direction. Gears 2 and 3 are rigidly connected to each other, and rotate freely about the dual shaft shown. Gear 1 also rotates freely about the dual shaft shown. Let R₁, R₂, R₃, R₄ be the radius of all the gears shown. Determine the angular velocity and angular acceleration of the dual shaft and gears 2 and 3.

Download solution

Problem # E-10:



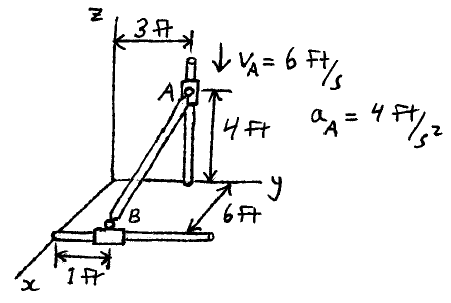
The rod AB has ball-and-socket joints at both ends which are attached to smooth collars A and B. Determine the angular velocity of the rod, and the velocity and acceleration of collar B at the instant shown.

Download solution

Problem # E-11:



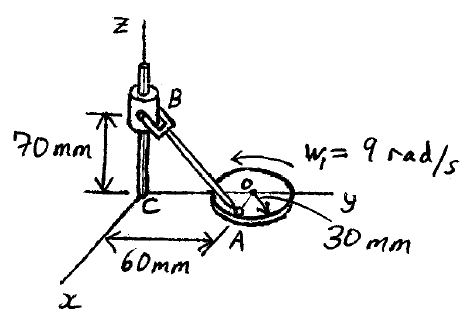
A rod AB is attached to a rotating disk at one end A with a ball-and-socket joint, and the other end B is attached to a clevis, which is attached to a collar that can slide along a vertical rod in the z-direction. The disk rotates in the xy-plane at a constant rate of w₁ = 9 rad/s. Determine the angular velocity of the rod, and the velocity of the collar at the instant shown.

Download solution

Problem # E-12:



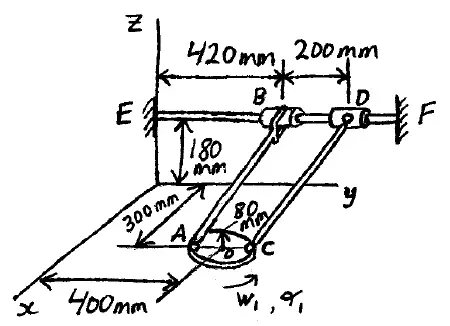
A rod AB and a rod CD are attached to a rotating disk with a ball-and-socket joint at one end. At the other end, rod AB is attached to a clevis, which is attached to a collar that can slide along a horizontal rod EF, in the y-direction. The other end of rod CD is attached to another collar with a ball-and-socket joint, and this collar can also slide along the rod EF. The disk rotates in the xy-plane at an angular velocity of w₁ = 8 rad/s, and at an angular acceleration of α₁ = 7 rad/s². Determine the velocity and acceleration of both collars, and determine the angular velocity and angular acceleration of rod AB and rod CD, at the instant shown.

Download solution

Problem # E-13:



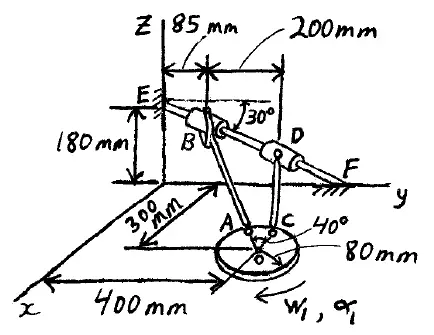
A rod AB and a rod CD are attached to a rotating disk with a ball-and-socket joint at one end. At the other end, rod AB is attached to a clevis, which is attached to a collar that can slide along a rod EF. The other end of rod CD is attached to another collar with a ball-and-socket joint, and this collar can also slide along the rod EF. The disk rotates in the xy-plane at an angular velocity of w₁ = 8 rad/s, and at an angular acceleration of α₁ = 7 rad/s². Determine the velocity and acceleration of both collars, and determine the angular velocity and angular acceleration of rod AB and rod CD, at the instant shown.

Download solution

Problem # E-14:



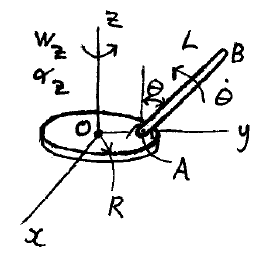
A disk is rotating about the z-axis with an angular velocity of w_z = 0.85 rad/s, and an angular acceleration of α_z = 1.5 rad/s², as shown. At the same instant, a rod AB that is connected to the disk, is rotating upward at a constant rate of dθ/dt = 0.7 rad/s. If θ = 40°, the disk radius is R = 2 ft, and the rod length is L = 5 ft, what is the velocity and acceleration of the rod tip B at the instant shown?

Download solution

Problem # E-15:



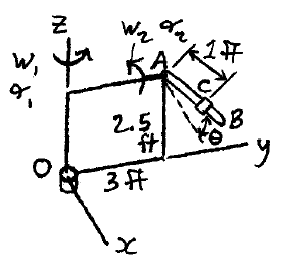
A rectangular plate is rotating about the z-axis with an angular velocity of w₁ = 0.8 rad/s, and an angular acceleration of α₁ = 1.2 rad/s², as shown. At the same instant, a rod AB that is connected to the plate, is rotating relative to the plate at an angular velocity of w₂ = 2 rad/s and an angular acceleration of α₂ = 3 rad/s². If θ = 30°, the plate side lengths are 3 ft and 2.5 ft, the distance between the collar C and point A is 1 ft, and C slides towards A with a velocity of 1.5 ft/s and a deceleration of -2.1 ft/s², both measured relative to the rod, what is the velocity and acceleration of the collar C at the instant shown?

Download solution

Problem # E-16:



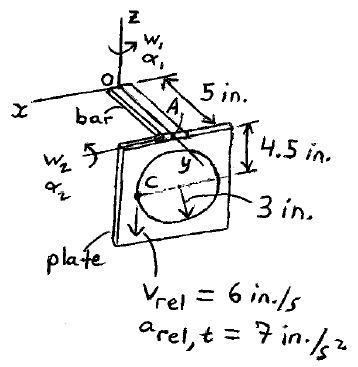
A bar is rotating about the z-axis with an angular velocity of w₁ = 2 rad/s, and an angular acceleration of α₁ = 3 rad/s², as shown. At the same instant, a plate that is connected to the bar, is rotating relative to the bar at an angular velocity of w₂ = 4 rad/s and an angular acceleration of α₂ = 5 rad/s². If a ball C is sliding along the edge of a circular hole cut into the plate, with a velocity of 6 in./s and a tangential acceleration of 7 in./s², both measured relative to the plate, what is the velocity and acceleration of the ball C at the instant shown?

Download solution



Return to Example Mechanics Problems page


Return to Real World Physics Problems home page