About me and why I created this physics website.

Hooke's Law

Hooke's Law states that the force acting on a spring is directly proportional to its displacement from its equilibrium position (as long as the spring does not exceed its elastic limit).

Mathematically, Hooke's law states that



Where:

F_s is the force exerted by the spring

k is the spring constant

x is the spring displacement from the equilibrium position, where the spring force F_s is zero


The figure below illustrates three cases, where a spring is attached to a (stationary) wall on the left and a moving particle (or body) on the right. The three cases are: (1) The spring is unstretched, (2) The spring is stretched, and (3) The spring is compressed. Note that the dashed line represents the equilibrium position of the spring.




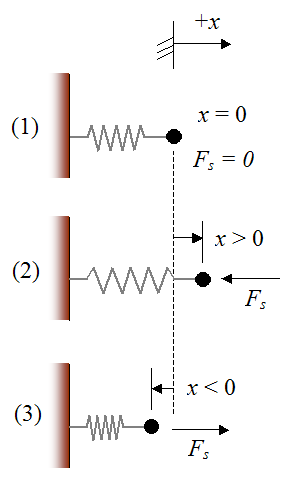
For case (1) the spring force F_s is zero because the spring is unstretched.

For case (2) the spring force F_s is pulling to the left because the spring is stretched to the right.

For case (3) the spring force F_s is pushing to the right because the spring is compressed to the left.


The force exerted by the spring is always in the direction opposite to its displacement from the equilibrium position. In other words, a spring always wants to return to its original position. As a result, the spring force F_s is commonly called a restoring force.


Using Calculus, we can determine the work done by the spring on the particle (or body) as it changes length between two positions. Let’s call these two positions 1 and 2.

For a force F that is parallel to displacement (x), the general equation for the work done by force F is equal to:



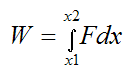
Substituting F_s into the above equation we have



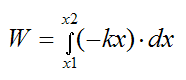
Integrating we have



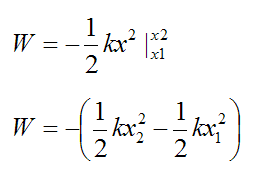
This is the work done by a spring on a particle (or body), from an initial spring displacement x₁ to a final spring displacement x₂.



Return to Dynamics page


Return to Real World Physics Problems home page