About me and why I created this physics website.

Impulse And Momentum

Principle Of Impulse and Momentum

Impulse is defined as the integral of a force acting on an object, with respect to time. This means that impulse contains the product of force and time. Impulse changes the momentum of an object. As a result, a large force applied for a short period of time can produce the same momentum change as a small force applied for a long period of time. An impulse can act on an object to change either its linear momentum, angular momentum, or both.

In many real life problems involving impulse and momentum, the impulse acting on a body consists of a large force acting for a very short period of time – for example, a hammer strike, or a collision between two bodies.

The following problem illustrates the principle of impulse and momentum.


A solid ball of mass m and radius r is rolling without slipping on a flat horizontal surface, at an initial angular velocity w₁. It hits a small bump of height h. What is the angular velocity of the ball immediately after impact? Also, what is the minimum initial angular velocity w₁ so that the ball just makes it over the bump? What is the minimum initial speed of the ball?

Assume that the ball pivots about the tip of the bump during, and after impact.




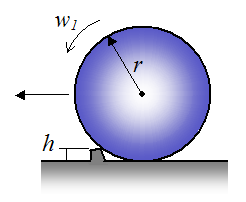
Solution

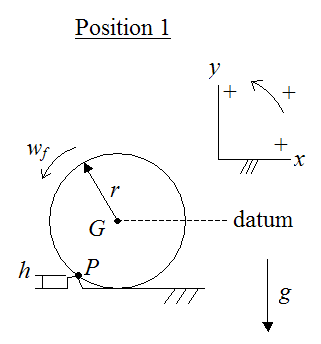
Set up a schematic of this problem, as shown, along with sign convention. Assume the center of mass G is at the geometric center of the ball. Gravity g is pointing down. During impact the ball is assumed to pivot about P, as indicated.



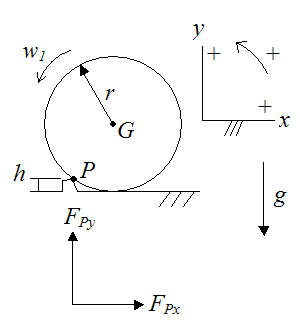
Let F_px be the horizontal impulse force at point P, and F_py be the vertical impulse force at point P.

We can treat this as a planar motion problem. It can be solved using the principle of impulse and momentum. Since this problem combines translation and rotation we must apply the equations for linear momentum and angular momentum.


In an impact of very short time duration (say, between an initial time t_i and a final time t_f), the impact force F_imp is typically very large. This means that the impulse term given by



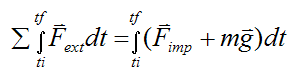
is dominated by the impact force F_imp, since mg (the gravitational force) is much smaller than F_imp. Therefore, we can ignore gravity for the impulse calculation.


For planar motion in the xy plane, the equations for impulse and linear momentum are:



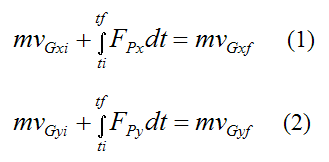
Where:

v_Gxi is the velocity of the center of mass G in the x-direction before impact, and v_Gxf is the velocity of the center of mass G in the x-direction after impact

v_Gyi is the velocity of the center of mass G in the y-direction before impact, and v_Gyf is the velocity of the center of mass G in the y-direction after impact

The integrals are the impulse terms.


Since the ball initially rolls without slipping,



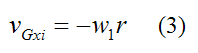
The negative sign accounts for the fact that positive angular velocity means the ball rolls to the left (in the negative x-direction).

Since the ball initially rolls on a flat horizontal surface,




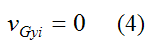
Immediately after impact the ball pivots about point P on the tip of the bump with an angular velocity w_f. As a result the velocity of the center of mass (v_Gf), after impact, is perpendicular to the line joining point G to point P.



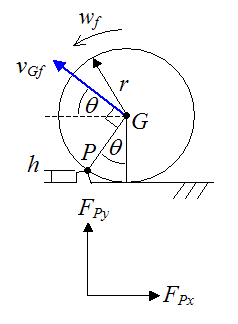
Since the ball pivots about point P immediately after impact:



From geometry we can write



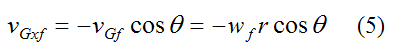
and



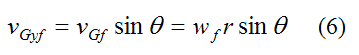
Substituting equations (3)-(6) into equations (1) and (2) we get




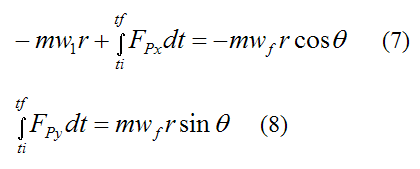
Now, for planar motion, the equation for impulse and angular momentum is:



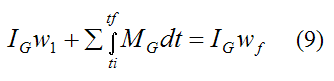
Where:

I_G is the moment of inertia of the ball about the center of mass G

ΣM_G is the sum of the moments about point G


Now, referring to the figure above we can write



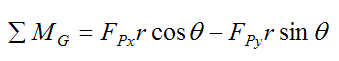
Thus,



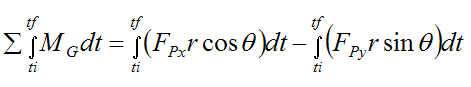
This can be written as



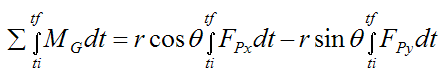
Substituting the above equation into equation (9) we get



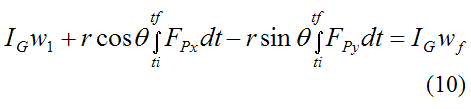
We can combine the three equations (7), (8), and (10) to solve for the three unknowns:



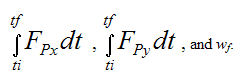
However, we only need to know w_f. Solving, we get



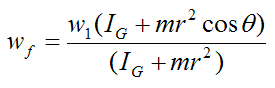
Now, by geometry



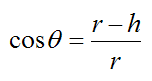
The moment of inertia of the solid ball about G is:



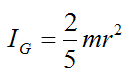
Substitute the above two equations into the equation for w_f and we get



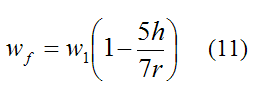
This is the angular velocity of the ball immediately after impact.


We now need to find the necessary initial angular velocity w₁ so that the ball just makes it over the bump.

We can use conservation of energy after impact since the only force that does work on the ball after impact is the gravitational force (which is a conservative force).

In the figure below, let’s define position 1 of the ball as its position immediately after impact. Due to the very short time of impact, this position very closely coincides with the position of the ball just as it touches the tip of the bump at point P, while rolling on the flat surface. Define the datum as coinciding with the initial height of the center of mass G of the ball as it is rolling on the flat surface.




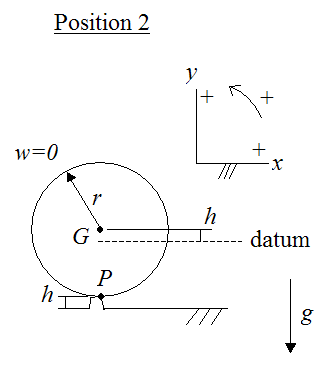
In the figure below, let’s define position 2 of the ball as its top-most position while it pivots about point P. If the ball is able to reach this top-most position it will roll down the bump on the other side. We wish to find the minimum initial angular velocity w₁ so that the ball is barely able to make it to the top of the bump. This corresponds to a kinetic energy of zero at the top of the bump.




Between positions 1 and 2, the equation for conservation of energy is:



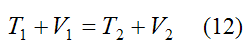
Where:

T₁ is the initial kinetic energy of the ball

V₁ is the initial potential energy of gravity acting on the ball

T₂ is the final kinetic energy of the ball

V₂ is the final potential energy of gravity acting on the ball


The initial kinetic energy of the ball is:



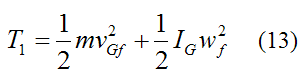
The initial potential energy of gravity acting on the ball (measured from the datum) is:



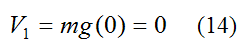
The final kinetic energy of the ball is:



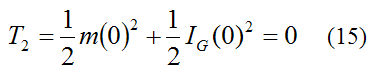
The final potential energy of gravity acting on the ball (measured from the datum) is:




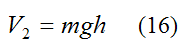
Substituting equations (13)-(16) into equation (12) we get




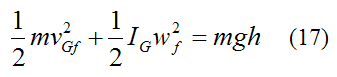
From before,



and




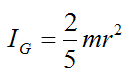
Substitute the above two equations into equation (17), and we get




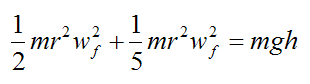
Solving for w_f we get




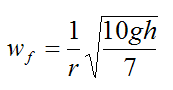
Substituting this equation into equation (11) and solving for w₁ we get



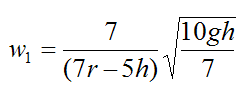
This is the minimum initial angular velocity so that the ball just makes it over the bump.

The minimum initial speed of the ball v₁ is:




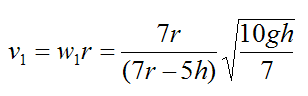
Comment

It’s interesting that when solving for w_f immediately after impact, we do not need to solve for F_px and F_py in the impulse terms:




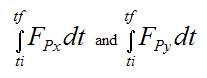
If we wanted to solve for F_px and F_py we would need more information, such as the impact time, and the material properties of the bump and ball. Fortunately, for many problems involving impulse and momentum, this isn’t necessary.



Return to Dynamics page


Return to Real World Physics Problems home page