Linear Momentum

The linear momentum for a system of particles can be derived from Newton’s Second Law. For a system of particles, this law states that:

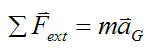
Where:

ΣF_ext is the vector sum of the external forces acting on the system of particles. This sum is sometimes called the net external force

m is the total mass of the system of particles

a_G is the acceleration of the center of mass G of the system of particles, with respect to an inertial reference frame (ground). This acceleration is a vector in the direction of the net external force

Note that there is no restriction in the way the particles are connected. As a result, the above equation will also hold true for a rigid body, a deforming body, a liquid, or a gas system.

Now, we can rewrite the above equation as

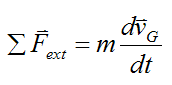
where v_G is the velocity of the center of mass G of the system of particles, with respect to an inertial reference frame (ground).

The above equation can be expressed as

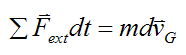
Integrating both sides from time t_i to time t_f we have

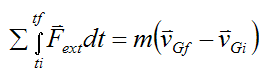
which becomes

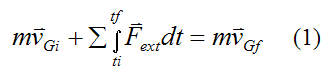
The term

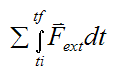
is defined as the external linear impulse acting on the system of particles (between t_i and t_f), due to the sum of the external forces acting on the particles.

We define the linear momentum for the system of particles as

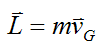
Therefore, equation (1) can be written as

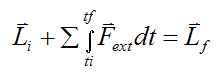
Note that there is no restriction in the way the system of particles are connected. As a result, the above equation will also hold true for a rigid body, a deforming body, a liquid, or a gas system. To see an example problem involving impulse and linear momentum see Rocket Physics.

If no external forces act on the system of particles, then

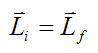
Linear momentum is therefore conserved for the system of particles (between t_i and t_f).

Return from Linear Momentum to Dynamics page

Return from Linear Momentum to Real World Physics Problems home page