About me and why I created this physics website.

Mousetrap Car Physics

A mousetrap car uses the stored energy of a mousetrap spring to generate forward motion. In competitions, the goal of the mousetrap car is to achieve as much forward motion as possible, on a flat surface and/or on an inclined surface. In other words, the goal is to maximize the distance traveled on both these surfaces.

I will discuss some of the physics of mousetrap powered cars as well as provide some design tips for building one.

To maximize the distance traveled on a flat surface, the friction (internal and external) and the weight of the car must be kept as small as possible. Specifically, this means that:

• All the components of the mousetrap car must weigh as little as possible, while being strong enough for use in the car. This can be accomplished by removing unnecessary material, such as by drilling holes in the components such as the frame and wheels.

• The wheels must be rigid and thin to minimize rolling resistance with the floor (or ground). But the drive wheels must additionally provide enough traction so that they don't slip when the car is accelerating.

• The frontal area of the car must be as small as possible to minimize air resistance. Although this will be much less than rolling resistance, every little bit helps.


To maximize distance traveled on a flat surface, the diameter of the drive wheels must be as large as possible to slow down the energy release of the spring. In order for the spring to release all its energy, the spring force must be able to turn the drive wheels throughout the range of motion of the spring, as the car travels on the flat surface. The drive wheel diameter must be as large as possible while allowing the spring to release all its energy. But if the drive wheel diameter is too large, the spring will get "stuck" at some intermediate position and the force transmitted to the ground/floor will be too low to move the car forward. You have to determine the ideal drive wheel diameter with trial and error.

Releasing the spring energy slowly, by way of larger drive wheels, has two key advantages. The first advantage is that it prevents slipping of the drive wheel on the ground/floor as the car accelerates. The second advantage is that the car takes longer to gain speed (accelerate) which results in it traveling farther than a car that gains speed faster. To understand this, consider the following energy equation, which equates the stored spring energy to the kinetic energy gained by the car: U_spring = (1/2)mV², where U_spring is the spring energy, m is the mass of the car, and V is the velocity of the car right after the spring has released all its energy. However, it is worth mentioning that this equation is an approximation, for two reasons: First, it assumes that there are no friction losses. Secondly, it doesn't account for the rotational motion of the wheels. This equation assumes that the mousetrap car is a fully rigid object. But as it turns out, these assumptions don't change the form of the energy equation and therefore don't affect the validity of my next important point.

In the above equation, we see that V is always constant regardless of how fast the car gains speed (keeping everything else the same). It follows that the car travels farther the longer it takes to reach V. After the car reaches V it will coast until it finally stops. But the coasting distance (after V is reached) will be roughly constant, so the biggest influence on distance traveled on a flat surface is how long it takes the car to gain speed.


Use old cds or old records for the wheels and use light, strong wood for the frame. Attach the mousetrap spring to a big flywheel which has nylon fishing line wound around it. This line from the flywheel is also wound around the drive wheel axle. When the mousetrap spring is released, it turns the flywheel which then turns the drive wheel axle which propels the car forward. You can use low friction bushings for the insertion holes (in the frame) into which the axles go. Use lubrication also.

You should use different sized wheels for the drive wheels depending on if the car is traveling on a flat surface or up an incline. As mentioned, larger drive wheels are best for traveling on a flat surface. But smaller drive wheels are better for going up an incline. The drive wheels must be small enough so that the spring force can turn the wheels throughout the range of motion of the spring (as the car travels up the incline). This allows the spring to release all its energy without getting "stuck" in some intermediate position. There is no lower limit on how small the drive wheels must be. Simply speaking, they must be small enough for the spring to release all its energy as the car travels up the incline. This is something that you have to determine by trial and error.

The dominant forces on the incline are gravity and the spring force, and by conservation of energy, the vertical distance traveled by the car can be approximated by equating the stored spring energy to the gravitational potential energy gained by the car. Mathematically, we can write U_spring = mgh, where g is the acceleration due to gravity, which is 9.8 m/s² on earth, and h is the vertical distance traveled on the incline. Note that this equation is an approximation because it assumes that there are no friction losses. Interestingly, we see from this equation that the distance traveled up the incline does not depend on the drive wheel diameter. This is true as long as the drive wheels are small enough so that the spring force can turn the wheels throughout the range of motion of the spring (as the car travels up the incline).

You can design the mousetrap car so that you have the smaller drive wheels on one end (which are suitable for the incline), and the larger drive wheels on the other end (which are suitable for the flat surface). And you can easily switch between the two.

The figure below shows a basic concept design for the mousetrap car, based on what was talked about here.



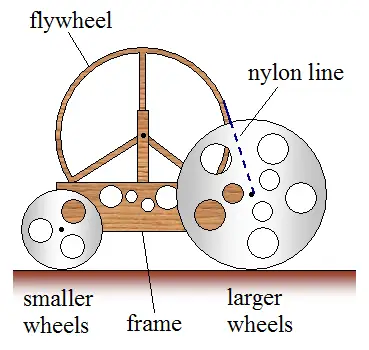
The exact type of mechanism needed to transfer the spring energy into forward motion of the car does not matter as long as it enables the spring to release all its energy as the car moves. For example, this mechanism could be a flywheel (as described here) or a long rod attached to the spring, which turns the axle and the drive wheels. Or it could be some other type of mechanism. If you decide to use a rod then its center of mass must rise and fall by the same amount as it "swings" through its range of motion. As a result, the net (gravitational) energy contribution of the rod to the system will be zero. Alternatively, the rod can be cleverly set up so that its center of mass falls by a net amount as it "swings" through its range of motion. This will add extra energy to the mousetrap car and it will travel farther as a result. However, this will probably be considered cheating.

There are different variables to consider, making the mousetrap car a challenge to design. It is fun though, and I learned from the experience when I did it for my third year design project. Make sure to test it thoroughly. The last thing you want is to have a good design which fails because of some silly oversight which no one thought of; such as the car not going straight and veering off course! You have to balance practical considerations with theoretical ones.



Return to Miscellaneous Physics page


Return to Real World Physics Problems home page