About me and why I created this physics website.

Newton's Second Law

Newton's second law states that, when a force acts on a particle, this force is equal to mass times acceleration.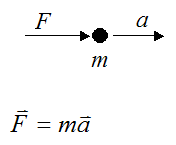



Where:

F is the vector force acting on the particle

m is the mass of the particle

a is the acceleration of the particle with respect to an inertial reference frame (ground) in the direction of the force (this is also a vector)


We can also write Newton's second law for a system of particles:



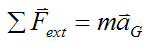
Where:

ΣF_ext is the vector sum of the external forces acting on the system of particles. This sum is sometimes called the net external force.

m is the total mass of the system of particles

a_G is the acceleration of the center of mass of the system of particles, with respect to an inertial reference frame (ground). This acceleration is a vector pointing in the same direction as the net external force.


Note that there is no restriction in the way the system of particles are connected. As a result, the above equation will also hold true for a rigid body, a deforming body, a liquid, or a gas system.

The above equation can be proven as follows.

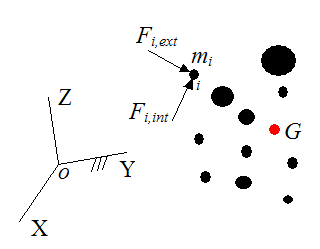
Define the following, as shown in the figure below:

Let XYZ represent an inertial reference frame.

Let point G represent the center of mass of the system of particles, represented by the red dot (shown below).

Let F_i,ext represent an external force (a vector) acting on particle i. An external force is a force that acts “externally” to a particle. It is due to “outside” contact, such as with another object that is not considered part of the system of particles.

Let F_i,int represent an internal force (a vector) acting on particle i. An internal force acts internally, and is due to contact with other particles in the system. Internal forces show up in equal and opposite pairs in a system of particles (by Newton's third law).

Let m_i represent the mass of particle i.

Let a_i represent the acceleration of particle i with respect to an inertial reference frame (ground). This acceleration is a vector.




For each particle i in the system we can write



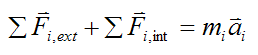
If we sum this equation over every particle in the system we have



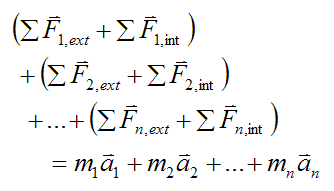
where n is the number of particles in the system.

On the left side of the above equation all the internal forces cancel out (since they are equal and opposite). This leaves us with only the external forces acting on the system of particles. Thus we have,



The right side of this equation can be replaced with the total mass of all the particles in the system times the acceleration of the center of mass. Therefore,



This is the result we set out to prove.

Note that the center of mass of a system of particles can be a point in empty space. It does not need to be at the location of a particle.

See the page on center of mass to see how to determine the location of the center of mass of a system of particles.

If you prefer to learn with a video, here is one in which I explain Newton's second law as it applies to a system of particles.





Return to Dynamics page


Return to Real World Physics Problems home page