About me and why I created this physics website.

Rectilinear Motion

Rectilinear motion is another name for straight-line motion. This type of motion describes the movement of a particle or a body.

A body is said to experience rectilinear motion if any two particles of the body travel the same distance along two parallel straight lines. The figures below illustrate rectilinear motion for a particle and body.


Rectilinear motion for a particle:




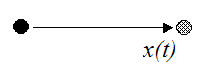
Rectilinear motion for a body:




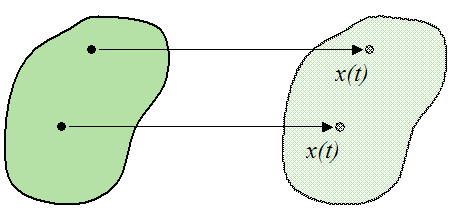
In the above figures, x(t) represents the position of the particles along the direction of motion, as a function of time t.

Given the position of the particles, x(t), we can calculate the displacement, velocity, and acceleration. These are important quantities to consider when evaluating the kinematics of a problem.

A common assumption, which applies to numerous problems involving rectilinear motion, is that acceleration is constant. With acceleration as constant we can derive equations for the position, displacement, and velocity of a particle, or body experiencing rectilinear motion.

The easiest way to derive these equations is by using Calculus.

The acceleration is given by



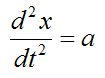
where a is the acceleration, which we define as constant.

Integrate the above equation with respect to time, to obtain velocity. This gives us



where v(t) is the velocity and C₁ is a constant.

Integrate the above equation with respect to time, to obtain position. This gives us



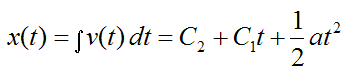
where x(t) is the position and C₂ is a constant.


The constants C₁ and C₂ are determined by the initial conditions at time t = 0. The initial conditions are:

At time t = 0 the position is x₁.

At time t = 0 the velocity is v₁.

Substituting these two initial conditions into the above two equations we get



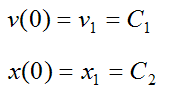
Therefore C₁ = v₁ and C₂ = x₁.


This gives us




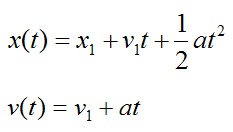
For convenience, set x(t) = x₂ and v(t) = v₂. As a result




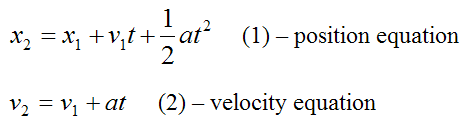
Displacement is defined as Δd = x₂−x₁. Therefore, equation (1) becomes




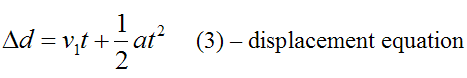
If we wish to find an equation that doesn’t involve time t we can combine equations (2) and (3) to eliminate time as a variable. This gives us




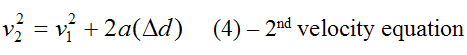
Equations (1), (2), (3), and (4) fully describe the motion of particles, or bodies experiencing rectilinear (straight-line) motion, where acceleration a is constant.

For the cases where acceleration is not constant, new expressions have to be derived for the position, displacement, and velocity of a particle. If the acceleration is known as a function of time, we can use Calculus to find the position, displacement, and velocity, in the same manner as before.

Alternatively, if we are given the position x(t) as a function of time, we determine the velocity by differentiating x(t) once, and we determine the acceleration by differentiating x(t) twice.

For example, let's say the position x(t) of a particle is given by



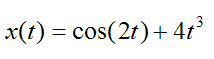
Thus, the velocity v(t) is given by



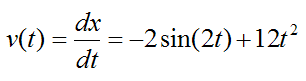
The acceleration a(t) is given by





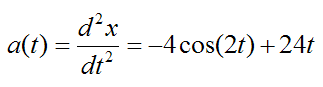
Return to Kinematics page


Return to Real World Physics Problems home page