About me and why I created this physics website.

Rolling

Pure Rolling Without Slipping

Consider a wheel that rolls on a surface, without slipping, as shown below.





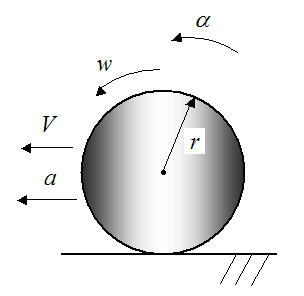
Where:

α is the angular acceleration of the wheel, in radians/s²

w is the angular velocity of the wheel, in radians/s

r is the radius of the wheel

V is the linear velocity of the geometric center of the wheel

a is the linear acceleration of the geometric center of the wheel

Thus,





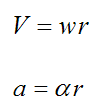
Rolling With Slipping

In the case of rolling with relative slipping, there is relative sliding at the contact between wheel and surface. This means that





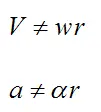
Dynamics problems that involve rolling with relative slipping are more complicated than problems that involve pure rolling. This is because you have to account for the direction of slip in order to determine the direction of (kinetic) friction, at the contact surface. To see an example of a solved problem that involves rolling with relative slipping, see The Physics Of Billiards. Scroll down near the end of the page to the section entitled: "A Closer Look At Relative Slipping". In this section, general equations are given for rolling with relative slipping, on a flat surface. It is useful to study this section, and then use the results for similar problems that you run into.



Return to Useful Physics Formulas page


Return to Real World Physics Problems home page