About me and why I created this physics website.

Work

Work is defined as the amount of energy transferred by a force, acting over a distance. It is a scalar quantity. Work is a very useful concept when solving problems using energy analysis (as will be explained).

Work Done On A Particle

To mathematically illustrate the concept of work for a particle, suppose we have a constant force F acting on a particle, which travels a distance Δs in the same direction as the force.



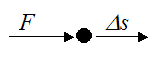
The work W done on the particle by the force is given by:



In this case the work done is simply the force (F) times the distance (Δs).


Now suppose we have a constant force F acting at an angle θ to the distance Δs. The work done is evaluated by taking the component of F acting in the same direction as Δs.



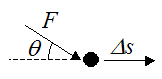
The work done on the particle by the force is given by:



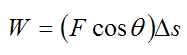
This is the same result as before, except that we are now taking the component of F along the direction Δs.


Let’s now consider the most general case where the force F is not constant (it changes with time), and it acts at an angle θ to the direction of travel Δs of the particle. Note that this angle can also change with time.



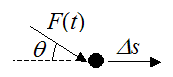
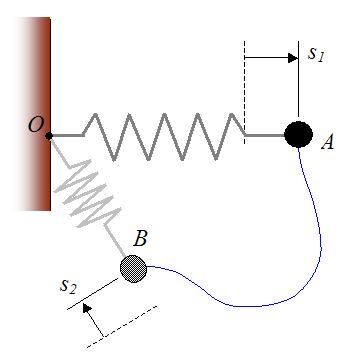
Using Calculus, we can set up a general expression for the work done by the force vector F(t) acting on the particle as the particle moves between two positions. Call these two positions A and B. The path traveled between A and B is arbitrary, and is represented by the blue curve, shown below.

Let the distance Δs be infinitesimally small, so that it lies tangent to the curve at the point where the particle is located.




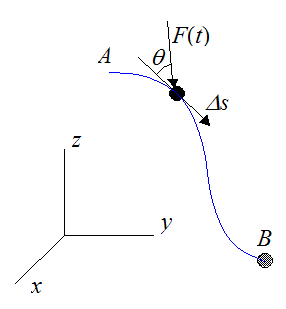
At the point where the particle is located, let dW represent the infinitesimally small work done on the particle over the distance Δs, and let Δs → ds. Thus,



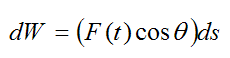
To evaluate the total work done on the particle between A and B we must take the integral of dW between A and B. Therefore,



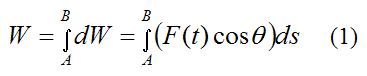
Now, F(t)cosθ is the component of the force F(t) that is tangent to the curve at the point where the particle is located. Therefore, by Newton’s Second Law, F(t)cosθ is equal to the mass of the particle times its acceleration component tangent to the curve, and relative to an inertial reference frame (ground). Thus,



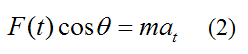
where m is the mass of the particle, and a_t is the acceleration component of the particle that is tangent to the curve, at the point where the particle is located.

Substituting equation (2) into equation (1) we get



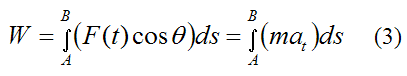
Now, the velocity of the particle is always tangent to the curve. If we set v as the magnitude of the particle velocity, then



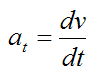
Using the chain rule of Calculus we can write



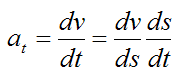
Since,



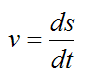
we can write



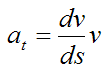
This gives us




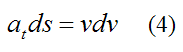
Substituting equation (4) into equation (3) we get



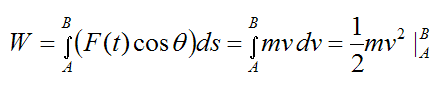
As a result,



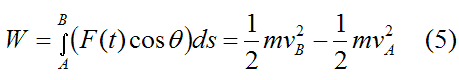
This scalar equation tells us that the work done on the particle between A and B is equal to the change in kinetic energy of the particle between A and B.

Once again, the term



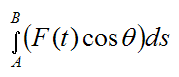
is equal to the work done by the forces acting on the particle. These forces can either be conservative or non conservative. The force F(t) is the resultant of these forces.


If gravity is acting on the particle, the work done by gravity is given by



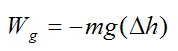
Where:

m is the mass of the particle

g is the acceleration due to gravity

Δh is the change in vertical height of the particle as it moves from A to B. Δh = h_B − h_A.




If an elastic spring (obeying Hooke's Law) is acting on the particle, the work done by the spring is



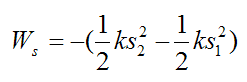
Where:

k is the spring constant

s₁ is the amount the spring is stretched or compressed from its equilibrium (unstretched) length, at position A

s₂ is the amount the spring is stretched or compressed from its equilibrium (unstretched) length, at position B




Thus, if gravity and an elastic spring are the only forces acting on the particle then



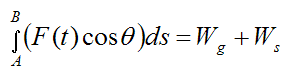
This tells us that you do not need to go through the effort of evaluating the integral on the left side of the above equation if the forces acting on the particle are gravity and/or an elastic spring. The work done by these two forces is simply given by the above equations for W_g and W_s. Both gravity and an elastic spring are conservative forces. As shown here, the work done by conservative forces can be easily calculated, without having to evaluate the integral in the above equation.



Work Done On A Rigid Body

To determine the work done by a force on a rigid body we must first treat the rigid body as a collection of particles and then sum the work done on each of those particles, in order to find the total work done on the rigid body.

For each particle in the rigid body we can apply equation (5), without loss of generality. Thus, for each particle in the rigid body (denoted by subscript i) we can write:



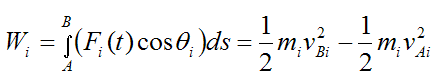
Summing over the entire rigid body we have:



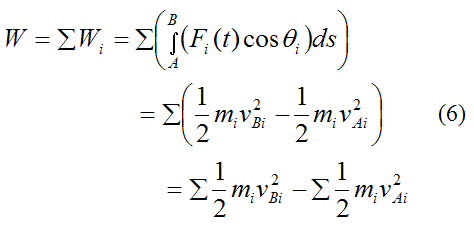
By Newton’s Third Law all internal forces cancel out. Therefore the term



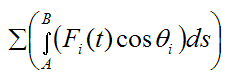
is equal to the work done only by the external forces (F_ext) acting on the rigid body. Thus,



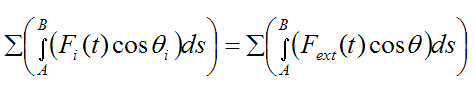
From the page on kinetic energy, the general kinetic energy equation for a rigid body at any instant is given by



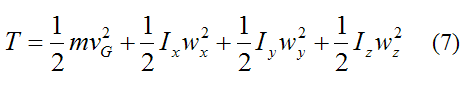
where the variables are defined on the page on kinetic energy.

Set



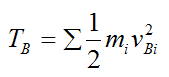
Therefore from equation (7),



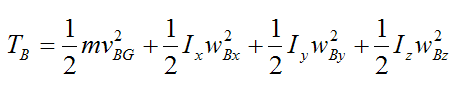
Set



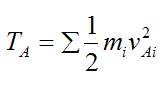
Therefore from equation (7),




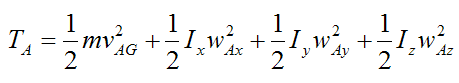
As a result equation (6) becomes



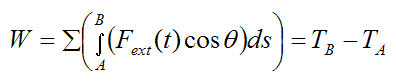
This scalar equation tells us that the work done on the rigid body by external forces (between A and B) is equal to the change in kinetic energy of the rigid body (between A and B). Note that equation (7) is the most general equation for kinetic energy of a rigid body experiencing motion in three dimensions. However, if the rigid body is experiencing, say planar motion, simpler equations can be used for kinetic energy. These equations are given on the page on kinetic energy.

Once again, the term



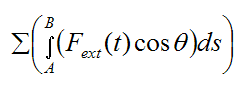
is equal to the work done by the external forces acting on the rigid body. These forces can either be conservative or non conservative.


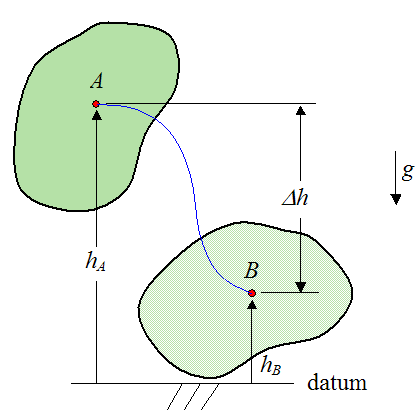
If gravity (an external force) is acting on the rigid body then the work done by gravity is given by



Where:

m is the mass of the rigid body

g is the acceleration due to gravity

Δh is the change in vertical height of the center of mass of the rigid body as it moves from A to B. Δh = h_B − h_A.




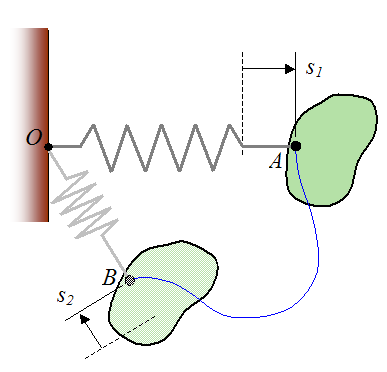
If an elastic spring (obeying Hooke's Law) is acting on the rigid body, the work done by the spring is



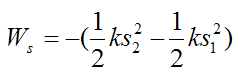
Where:

k is the spring constant

s₁ is the amount the spring is stretched or compressed from its equilibrium (unstretched) length, at position A

s₂ is the amount the spring is stretched or compressed from its equilibrium (unstretched) length, at position B




Thus, if gravity and an elastic spring are the only forces acting on the rigid body then



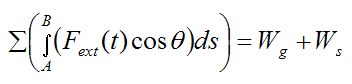
This tells us that you do not need to go through the effort of evaluating the integral on the left side of the above equation if the (external) forces acting on the rigid body are gravity and/or an elastic spring. The work done by these two forces is simply given by the above equations for W_g and W_s. Both gravity and an elastic spring are conservative forces. As shown here, the work done by conservative forces can be easily calculated, without having to evaluate the integral in the above equation.



Special Case: Body Undergoing Planar Motion – Work Of A Force Couple

Suppose there are two parallel forces F_c acting in the plane of motion of a body, and located anywhere on the body. These forces are acting in opposite directions, and R is the perpendicular distance between these forces. This pair of forces is commonly called a force couple. They exert a pure moment on the body.



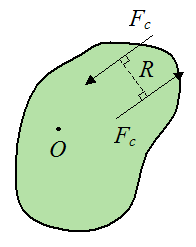
No matter where this force couple is located relative to an arbitrary point O, they will always exert the same moment on the body. They are a special case of moment of a force.

The direction of the moment due to this couple is given by the right hand rule and it is perpendicular to the plane containing the force pair. The magnitude of the moment M_o caused by the force couple is given by:



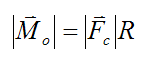
If the body rotates in the plane between two angles α₁ and α₂, the work done by M_o on the body is given by



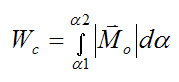
where α is measured in radians.

If M_o is constant then



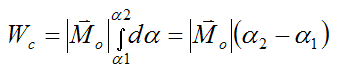
This formula can be useful for, say, determining the work done by a pure moment (torque) acting on a flywheel that rotates between angles α₁ and α₂.

Make sure you use the right hand rule to assign the correct sign for M_o and dα in the above equation (depending on their sense of rotation).



Forces That Do No Work

If a force acts perpendicular to the direction of travel it does no work. This is easy to see if one looks at the equation for work done by a force F acting on a particle, which acts at an angle θ to the distance traveled Δs.



The work is given by:



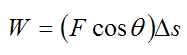
The force F acts perpendicular if θ = 90° . Therefore,




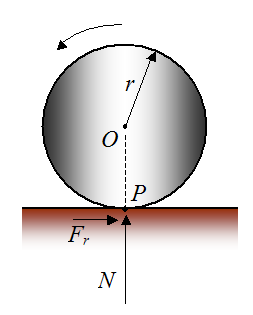
Another example of a force that does no work is the friction force acting on a wheel (or ball) that rolls without slipping, as shown below. The friction force acts at the contact point P of the wheel. Since this contact point is stationary (zero velocity), due to the no slip condition, the force F_r does no work. On the other hand, if there was rolling with slipping then the force F_r would do work because of the relative motion at the contact point P.

However, whether or not there is slipping, the normal force N acting at point P always does zero work because it is always perpendicular (at 90°) to the relative motion (if any) at point P.





Power

Power is defined as the rate at which work is performed (with respect to time).


Power acting on a particle

If we know the instantaneous force F acting on a particle and the velocity v of the particle, we can calculate the instantaneous power P acting on the particle.




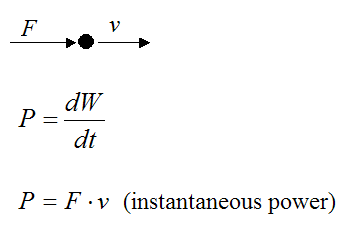
Power acting on a rigid body rotating about a fixed point

If we know the instantaneous torque τ acting on a rigid body and the angular velocity w of the rigid body (in radians/second), we can calculate the instantaneous power P acting on the rigid body.



A flywheel is an example of a rotating rigid body for which we might want to know the power acting on it.



In Closing

The usefulness of solving dynamics problems using work and energy calculations is that it can greatly simplify the analysis of some problems. You don’t have to draw a free body diagram and analyze the forces involved. Furthermore, there is only a single scalar equation to apply (for each particle, or for each rigid body), as opposed to applying force and moment equations for each of the three directions (x,y,z). This can significantly reduce the computation effort.



Return to Dynamics page


Return to Real World Physics Problems home page